¿QUE ES LA FÍSICA?
La física es la ciencia que estudia el comportamiento y las relaciones entre la materia, la energía, el espacio y el tiempo, podemos decir que la física investiga los fenómenos que ocurren en la naturaleza y en el universo con el objeto de establecer leyes matemáticas que puedan predecir su comportamiento.
IMPORTANCIA DE LA FÍSICA
La física es la ciencia que estudia la Naturaleza en su sentido más amplio. La física es la ciencia básica que estudia el cosmos, es decir, el todo desde el punto de vista científico. Aunque, aparentemente, la física consiste en buscar o encontrar una matematización de la realidad observable, no es así. Lo que ocurre es que la matemática es el idioma en que se puede expresar con mayor precisión lo que se dice en física
ÁREAS QUE SE RELACIONAN CON LA FÍSICA
1- Astronomía.: como se había mencionado anteriormente la física busca explicar fenómenos universales dentro de los cuales están los agujeros negros, las estrellas, la formación de galaxias, incluso la teoría del nacimiento de nuestro planeta.
2- Matemáticas: es una ciencia de soporte para la física pues se crean formulas y ecuaciones para representar fenómenos y leyes y también para la elaboración de cálculos y análisis.
3- Química: probablemente la ciencia más importante con las que se relaciona la física pues muchos de los fenómenos naturales son conjuntamente físico-químicos.
4- Biología: se le conoce como biofisica, y estudia fenómenos de la naturaleza, aplicando leyes físicas para entender y predecir su comportamiento.
5- Geología; o geofisica, estudian aspectos relacionado con el planeta pero de espectro físico como los campos electromagnéticos, ciclos evolutivos. gravedad.
EL MÉTODO CIENTÍFICO
El método científico es una metodología para obtener nuevos conocimientos, que ha caracterizado históricamente a la ciencia, y que consiste en la observación sistemática, medición, experimentación, y la formulación, análisis y modificación de hipótesis. Otras características del método científico son la deducción,2 la inducción, la abducción, la predicción, la falsabilidad, la reproducibilidad y repetibilidad de los resultados, y la revisión por pares.
PASOS DE MÉTODO CIENTÍFICO
Los pasos del método científico sirven para responder a una pregunta científica de una forma organizada y objetiva. Implica observar el mundo y sus fenómenos, llegar a una explicación de lo que se observa, probar si la explicación es válida, y finalmente aceptar o negar la explicación.
Observación: El primer paso de cualquier método científico será siempre la observación. Esta se podrá llevar a cabo directamente con los sentidos o mediante herramientas que nos ayuden a mejorar la percepción de la realidad observada, por ejemplo los telescopios
Hipótesis: La hipótesis es la explicación que se da a partir de las observaciones realizadas. De este modo, se presenta como una posible teoría. Sin embargo, habrá que tener en cuenta que una hipótesis siempre será una posibilidad, pero que será necesario reforzar mediante nuevos estudios, para lo que será necesario llevar a cabo una serie de experimentos.
Experimentación: Este paso es posterior a la hipótesis y su función principal será darle validez mediante experimentos que sirvan para demostrar la veracidad de la hipótesis planteada. En el caso de que los experimentos lleven a negar la hipótesis, será necesario descartarla y formular una nueva hipótesis que responda de forma satisfactoria a las observaciones llevadas a cabo durante la experimentación y la observación.
Teoría: Una vez que la experimentación haya servido para demostrar que la hipótesis planteada tiene sentido, se elaborará una teoría. La teoría será el resultado de aquellas hipótesis que tengan una probabilidad mayor de ser confirmadas como ciertas.
- Ley: Finalmente, en el caso de la teoría pueda ser demostrada mediante nuevas experimentaciones, la teoría pasará a convertirse en ley. En este caso, se trata de una certeza basada en la experiencia tanto de las observaciones como de los experimentos y el estudio teórico, por lo que se trata del último de los pasos del método científico con el que tendremos que trabajar, ya que estará sustentada por toda la información anterior de la que dispongamos.
PROBLEMAS DE LA DENSIDAD
Raquel trabaja en un laboratorio calculando la densidad de ciertos objetos. José le llevó a Raquel un objeto cuyo peso es 330 gramos y su capacidad es de 900 centímetros cúbicos. ¿Cuál es la densidad del objeto que José le dio a Raquel?
Como se dijo antes, la unidad de medida de la densidad también puede ser g/cm³. Por lo tanto, no hace falta hacer la conversión de unidades. Aplicando la definición anterior, se tiene que la densidad del objeto que José le llevó a Raquel es:
ρ= 330g / 900 cm³ = 11g / 30cm³=11/30 g/cm³.
PROBLEMA 2
Rodolfo y Alberto tienen cada uno un cilindro y quieren saber cuál cilindro tiene mayor densidad.
El cilindro de Rodolfo pesa 500 g y tiene un volumen de 1000 cm³ mientras que el cilindro de Alberto pesa 1000 g y tiene un volumen de 2000 cm³. ¿Cuál cilindro tiene mayor densidad?
Sea ρ1 la densidad del cilindro de Rodolfo y ρ2 la densidad del cilindro de Alberto. Al utilizar la fórmula para el cálculo de la densidad se obtiene:
ρ1= 500/1000 g/cm³ = 1/2 g/cm³ y ρ2= 1000/2000 g/cm³ = 1/2 g/cm³.
Por lo tanto, ambos cilindros tiene la misma densidad. Cabe destacar, que de acuerdo al volumen y al peso, se puede concluir que el cilindro de Alberto es más grande y más pesado que el de Rodolfo. Sin embargo, sus densidades son las mismas.
PROBLEMA 3
¿Cuál es la densidad de un árbol cuyo peso es de 1200 kg y su volumen es de 900 m³?
En este ejercicio solamente se pide calcular la densidad del árbol, es decir:
ρ= 1200kg / 900 m³ = 4/3 kg/m³.
Por lo tanto, la densidad del árbol es de 4/3 kilogramos por metro cúbico
MAGNITUDES FÍSICAS
NOTACIÓN CIENTÍFICA
El proceso de'notación científica, también denominada patrón y notación en forma exponencial, es una forma de escribir los números que acomoda valores demasiado grandes (100 000 000 000) o pequeños como puede ser el siguiente (0.000 000 000 01)1para ser escrito de manera convencional El uso de esta notación se basa en potencias de 104 (los casos ejemplificados anteriormente en notación científica, quedarían 1 × 1011 y 1 × 10−11, respectivamente). El módulo del exponente en el caso anterior es la cantidad de ceros que lleva el número delante, en caso de ser negativo (nótese que el cero delante de la coma también cuenta), o detrás, en caso de tratarse de un exponente positivo.
PARA MULTIPLICAR
Para multiplicar números en notación científica, por un lado se multiplican los números que están delante de la potencia de 10 y por otro, se multiplican las potencias de 10, manteniendo la base y sumando los exponentes.
Por ejemplo:
PARA SUMAR
Ahora lo queremos expresar con 10 elevado a -1. Al pasar de 10 elevado a 2 a 10 elevado a -1, estamos haciendo la potencia de 10 1000 veces más pequeña, por tanto, hay que hacer el número 1000 veces más grande, moviendo la coma 3 lugares hacia la derecha:
PARA DIVIDIR
Por un lado, dividimos los números y por otro las potencias de 10, manteniendo la base y restando los exponentes:

¿QUE ES LA MECÁNICA FÍSICA?
En fisica, se conoce como mecánica al estudio y análisis del movimiento y reposo de los cuerpos, así como su evolución temporal bajo la acción de una o varias fuerzas. Su nombre proviene del vocablo latino mechanica, que traduce “el arte de construir máquinas”, lo cual tiene sentido, dada la tendencia de esta disciplina de comprender los fenómenos y cuerpos de su interés a manera de sistemas.
¿QUE ES LA CINEMÁTICA?
La física es la ciencia básica encargada de estudiar las interacciones y características de la energía y la materia. Se puede definir del mismo modo, como el estudio de los fenómenos naturales entre los que se pueden destacar movimiento y la luz, por lo que también es reconocida como una de las ciencias más antiguas y complejas que existen.
MOVIMIENTO UNIFORME
Movimiento uniforme: Es aquel desplazamiento en el cual la velocidad del objeto o cuerpo que se desplaza permanece constante, cualquiera que sea su trayectoria (circular, lineal, pendular, elíptica, etc.); el movimiento uniforme es ampliamente verificable en cualquiera de sus vertientes como son el M.R.U (Movimiento rectilíneo uniforme), el M.R.U.A. (Movimiento rectilíneo uniformemente acelerado), el M.C.U. (Movimiento circular uniforme) o el M.C.U.A. (Movimiento circular uniformemente acelerado), en ejemplos de la vida diaria y en muchos campos de estudio como la astronomía y la balística.
Un automóvil Porsche de Carrera GT viaja en línea recta con una velocidad media de 1 300 cm/s durante 8 s, y luego con velocidad media de 480 cm/s durante 10 s, siendo ambas velocidades del mismo sentido:
|  |
a) ¿cuál es el desplazamiento total en el viaje de 18 s del automóvil Porsche?.
b) ¿cuál es la velocidad media del automóvil Porsche en su viaje completo?.
Solución
Datos:
| Momento 1 | Momento 2 |
|---|---|
| v1 = 1 300 cm/s | v2 = 480 cm/s |
| t1 = 8 s | t2 = 10 s |
a. El desplazamiento que el automóvil Posche hace en el mismo sentido, es:
Como la formula que utilizaremos es x = v.t
| Momento 1 | Momento 2 |
|---|---|
| x1 = (v1).(t1) | x2 = (v2).(t2) |
| x1 = (1 300 cm/s). (8 s) | x2 = (480 cm/s).(10 s) |
| x1 = 10 400 cm | x2 = 4 800 cm |
El desplazamiento total es:
Xt = X1 + x2
Xt = 10 400 cm + 4 800 cm
Xt = 15 200 cm = 152 m
Xt = X1 + x2
Xt = 10 400 cm + 4 800 cm
Xt = 15 200 cm = 152 m
Entonces el desplazamiento total a los 18 s del Porsche es: 15 200 cm = 152 m
b. La velocidad media del viaje completo del Porsche
Como el tiempo total es:
tt = t1 + t2 = 8 s + 10 s = 18 s
Con el desplazamiento total recién calculado aplicamos:
Δv = xtotal / ttotal
Δv = 152 m / 18 s
Δ v = 8.44 m/s
tt = t1 + t2 = 8 s + 10 s = 18 s
Con el desplazamiento total recién calculado aplicamos:
Δv = xtotal / ttotal
Δv = 152 m / 18 s
Δ v = 8.44 m/s
La velocidad media del automóvil Porsche en su viaje completo es 8.44 m/s
MOVIMIENTO RETILINIO UNIFORME VARIADO
En este tipo de movimiento a diferencia del MRU (movimiento rectilíneo uniforme), la velocidad varía. Pero esta variación a su vez es con un cierto orden, es decir que cambia un mismo intervalo en una misma cantidad de tiempo.
Por este hecho aparece una nueva magnitud llamada aceleración. La aceleración está representada por la fórmula:
a = (Vf – Vi) / T
La a es la aceleración, Vi es la velocidad del inicio y Vf es la velocidad final.
Para calcular la distancia recorrida se usa la siguiente fórmula:
D = Vi . T +/- ½ . a . T2
EJERCICIOS MOVIMIENTO RETILINIO
Datos:
Solución:
Podemos emplear la ecuación de la velocidad promedia que implica a la distancia, pues es más fácil sustituir nuestros datos y resolver.
Respuesta:
Datos:
Solución:
Aunque parezca un problema difícil, en realidad no lo es. Si sabemos que por cada 45 cajas en 1 minuto sale un pedido. Si necesitamos 3 pedidos en 2 minutos entonces aplicamos en la fórmula.
Es decir, que la velocidad de la transportadora forzosamente necesita ajustarse a 67.5 cajas por minuto para que a velocidad constante logre suministrar las 45 cajas en 3 pedidos cada 2 minutos.
Respuesta:
Datos:
Solución:
Sustituyendo directamente nuestros datos en la fórmula de la velocidad
TEOREMA SENO
Sea un triángulo cualquiera con lados , y y con ángulos interiores , y (son los ángulos opuestos a los lados, respectivamente).
Entonces, se cumple la relación
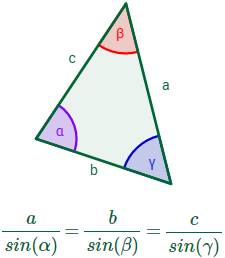
Además, se cumple
teorema del coseno:
denominado también como ley de cosenos,2 es una generalización del teorema de Pitágoras en los triángulos rectángulos en trigonometría.
El teorema relaciona un lado de un triángulo cualquiera con los otros dos y con el coseno del ángulo formado por estos dos lados:
|
MOVIMIENTO DE PROYECTILES
El movimiento de un proyectil es un ejemplo clásico del movimiento en dos dimensiones con aceleración constante. Un proyectil es cualquier cuerpo que se lanza o proyecta por medio de alguna fuerza y continúa en movimiento por inercia propia. Un proyectil es un objeto sobre el cual la única fuerza que actúa es la aceleración de la gravedad. La gravedad actúa para influenciar el movimiento vertical del proyectil. El movimiento horizontal del proyectil es el resultado de la tendencia de cualquier objeto a permanecer en movimiento a velocidad constante. | |
LANZAMIENTO HORIZONTAL
Un ejemplo de lanzamiento horizontal es el que se produce cuando una pelota rueda desde el extremo de una mesa horizontal y cae al suelo. Para simplif icar el análisis, se supone que el movimiento comienza en el tiempo  en el origen de un sistema de coordenadas
en el origen de un sistema de coordenadas  , donde
, donde  . En el momento en que la pelota abandona el borde de la mesa (
. En el momento en que la pelota abandona el borde de la mesa ( ) solo t iene la componente horizontal de la velocidad inicial (
) solo t iene la componente horizontal de la velocidad inicial ( ). Luego la pelota experimenta la aceleración de gravedad (
). Luego la pelota experimenta la aceleración de gravedad ( ) vertical hacia abajo, por lo que la componente vertical de la velocidad (
) vertical hacia abajo, por lo que la componente vertical de la velocidad ( ) que inicialmente era cero, comienza a aumentar continuamente hacia abajo.
) que inicialmente era cero, comienza a aumentar continuamente hacia abajo.
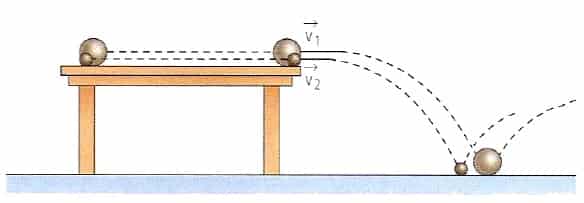
Lanzamiento horizontal.
En este caso, las ecuaciones del movimiento del proyectil se ven simplificadas de la siguiente forma:
- Horizontalmente, las ecuaciones son:De posición:
De velocidad:
- Verticalmente, las ecuaciones son:De posición:
De velocidad:De velocidad independiente del tiempo:
MOVIMIENTO SEMIPARABOLICO
En un movimiento semiparabólico, cuando un objeto es lanzado con cierta inclinación respecto a la horizontal y bajo la acción solamente de la fuerza gravitatoria su trayectoria se mantiene en el plano vertical y es parabólico. La resistencia del aire, la rotación de la tierra, etc., no introducen afectaciones apreciables.
Es importante considerar durante todo el recorrido la aceleración debido a que la gravedad permanece constante y que el movimiento solo es de traslación.
- El movimiento horizontal del objeto es rectilíneo y uniforme ya que en esa dirección la acción de la gravedad es nula y consecuente, la aceleración también.
- En la dirección vertical sobre el objeto actúa la fuerza de gravedad que hace que el movimiento sea rectilíneo uniformemente acelerado, con la aceleración constante.
- Los cuerpos se lanzan horizontalmente desde cierta altura y con una velocidad inicial (Vi)
- El movimiento en "x" es independiente del movimiento en y.
- El tiempo de caída es variable que relaciona a los dos movimientos (MU y MUA)
Las fórmulas utilizadas son:
x = Vox.t = Vo.cos θ.t
y = Voy.t – ½.g.t2 = Vo.sen θ.t – ½ gt2
vx = Vox
vy = Voy – g.t
El movimiento parabólico es una combinación de 2 movimientos: 1 movimiento rectilíneo uniforme en el eje «x»; y 1 movimiento de caída libre en el eje «y».

En la mayoría de problemas, tendrás que descomponer el movimiento parabólico en estos 2 movimientos para poder hallar las respuestas. Veamos ahora las fórmulas en cada uno de los ejes:
Eje «x» (Movimiento Rectilíneo Uniforme – MRU)
Aquí la fórmula con la que trabajaremos será la siguiente:
Donde:
- dx : distancia recorrida en el eje «x» o eje horizontal.
- Vx : velocidad en el eje «x».
- t : tiempo del recorrido.
Eje «y» (Movimiento de Caída Libre – MCL)
Mientras que en el eje «y» aplicaremos las siguientes fórmulas de caída libre:

Donde:
- Vfy : velocidad final en el eje «y»
- Voy : velocidad inicial en el eje «y».
- g : gravedad (en los problemas de hoy trabajaremos con 10m/s2.
- t : tiempo del recorrido.
Fórmulas adicionales
En este capítulo, existen además 4 fórmulas adicionales que nos ahorran mucho tiempo, y son las siguie
MOVIMIENTO CIRCULAR UNIFORME (M.C.U)
El movimiento circular uniforme (m.c.u.) es un movimiento de trayectoria circular en el que la velocidad angular es constante. Esto implica que describe ángulos iguales en tiempos iguales. En él, el vector velocidad no cambia de módulo pero sí de dirección (es tangente en cada punto a la trayectoria). Esto quiere decir que no tiene aceleración tangencial ni aceleración angular, aunque sí aceleración normal.
Eligiendo el origen de coordenadas para estudiar el movimiento en el centro de la circunferencia, y conociendo su radio R, podemos expresar el vector de posición en la forma:
De esta manera, la posición y el resto de magnitudes cinemáticas queda definida por el valor de φ en cada instante.
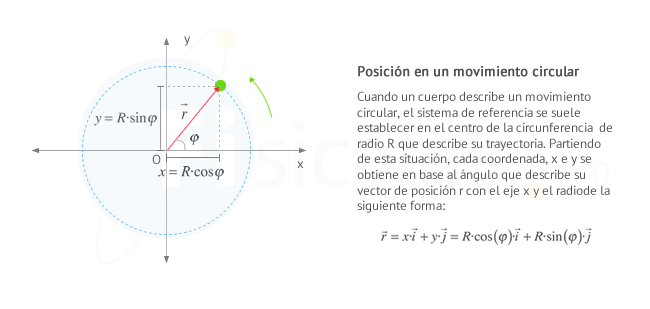
PARTES DE UN MOVIMIENTO CIRCULAR UNIFORME
Una vuelta a la circunferencia también se llama oscilación o revolución. Nota: Cada magnitud del MCU puede representarse de la misma manera en varias fórmulas diferentes, siendo cualquiera de ellas igualmente válidas. PERIODO. Es el tiempo que tarda la partícula en dar una vuelta completa. Se representa por "T" y se mide en segundos (seg): FRECUENCIA. Es la cantidad de vueltas que recorre la partícula en la unidad de tiempo (1 segundo). Se representa por "f" y se mide en 1/seg ó seg-1, que se llaman Herzios (Hz): 1 Hz = 1 seg-1 Entre el periodo y la frecuencia, se tiene que son inversos, o sea: VELOCIDAD. Existen dos tipos de velocidades: VELOCIDAD LINEAL: Es la velocidad propia de la partícula cuya magnitud es constante, pero su dirección cambia ya que siempre es tangente a la circunferencia.
V = velocidad lineal
R = radio de la circunferencia T = periodo f = frecuencia ω = velocidad angular
VELOCIDAD ANGULAR: Es el ángulo que se recorre en cierta cantidad de tiempo. Se representa con la lietra griega ω (omega minúscula), así:
ω = velocidad angular
θ = ángulo recorrido t = tiempo T = periodo f = frecuencia
Observación: La Velocidad Angular también se llama Frecuencia Angular, ya que ambas se miden en Herzios o seg-1.
ACELERACIÓN. En el MCU, la velocidad lineal permanece constante, y por lo tanto NO hay aceleración tangencial, sólo hay aceleración centrípeta:
aC = aceleración centrípeta
V = velocidad lineal R = radio de la circunferencia T = periodo f = frecuencia ω = velocidad angular
FUERZA CENTRÍPETA.
Es la fuerza necesaria para producir un Movimiento Circular Uniforme (MCU). Su dirección es perpendicular a la velocidad lineal y está dirigida hacia el centro de la circunferencia:
FC = fuerza centrípeta
m = masa de la partícula V = velocidad lineal R = radio de la circunferencia T = periodo f = frecuencia ω = velocidad angular
El efecto de la Fuerza Centrípeta es cambiar la dirección de la velocidad lineal sin cambiar su magnitud, produciendo la Aceleración Centrípeta.
Cuando una partícula con Movimiento Circular Uniforme (MCU) se suelta en un instante dado, ésta escapa por la línea tangente a ese punto y continúa con un Movimiento Continuo (MUC). Este escape se produjo por la acción de la llamada FUERZA CENTRIFUGA, la cual es consecuencia de la tercera ley de Newton (acción y reacción) de la Fuerza Centrípeta, es decir, mientras que la Fuerza Centrípeta apunta hacia el centro de la circunferencia, la Fuerza Centrífuga apunta en sentido opuesto, desde la partícula hacia el exterior. Ambas fuerzas, centrípeta y centrífuga, al poseer igual magnitud pero dirección opuesta, permiten que la partícula se escape con una dirección perpendicular a ellas, es decir, tangencialmente a la circunferencia. En la práctica, la fuerza centrípeta es la de mayor atención y análisis, más que la fuerza centrífuga.
TRANSMISIÓN DE CORREAS Y ENGRANAJES
Los engranajes y poleas provistas de correas son máquinas que permiten transmitir el movimiento de rotación de una rueda a otra. Las ruedas o engranajes tienen velocidades lineales iguales. Si sus radios son de diferente longitud, se obtienen velocidades angulares distintas entre las ruedas, dadas por la expresión:
ωA = velocidad angular de rueda o engranaje A
RA = radio de la rueda o engranaje A ωB = velocidad angular de rueda o engranaje B RB = radio de la rueda o engranaje B
De la fórmula, se deduce que: Las velocidades angulares de las dos ruedas son inversamente proporcionales a sus radios respectivos.
En la transmisión del movimiento, aparece una Ventaja Mecánica (V.M.) entre las dos ruedas: Entre mayor sea la velocidad angular menor es la fuerza que ejerce la rueda y viceversa, a menor velocidad mayor fuerza. De este modo, la V.M. es la razón dada por la expresión anterior con respecto a dos ruedas o engranajes. |
SEGUNDA LEY DE NEWTON
La segunda ley de Newton o principio fundamental establece que la rapidez con la que cambia el momento lineal (la intensidad de su cambio) es igual a la resultante de las fuerzas que actúan sobre él:
Donde:
∑F→ : Representa la fuerza total que actúa sobre el cuerpo en el intervalo de tiempo considerado. Su unidad de medida en el Sistema Internacional (S.I.) es el newton.Δp→ : Representa la variación del momento lineal producida en el intervalo de tiempo considerado. Se puede calcular como la diferencia entre su valor final y su valor inicial:Δp→=p→f−p→i , y recuerda quep→=m⋅v→ . Su unidad de medida en el S.I. es el kg·m/s.- Δt : Representa el intervalo de tiempo considerado. Su unidad de medida en el S.I. es el segundo
Como puedes ver, este principio relaciona matemáticamente las fuerzas con el efecto que producen, de tal forma que resulta fundamental para resolver cualquier problema de dinámica.
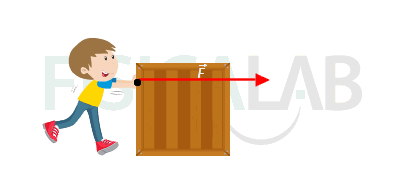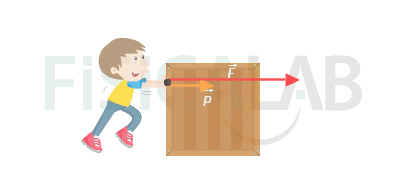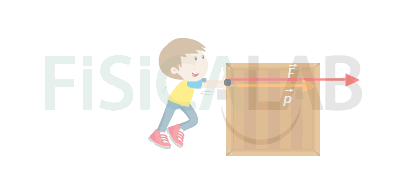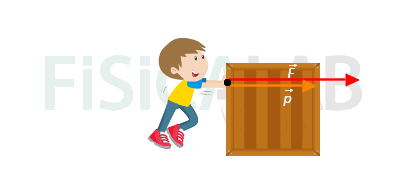
Ejemplo de aplicación de la segunda ley de Newton
Cuando empujas un objeto, por ejemplo una caja, aplicando una fuerza sobre él de manera sostenida, se produce un incremento de su momento lineal, representado por la flecha naranja. Ten presente que siempre que la masa a la que aplicas la fuerza se mantenga constante, el aumento del momento lineal se traducirá en un incremento de su velocidad, pues p=m·v.
Solución: En el ejemplo, tenemos prácticamente nuestros datos, que es lo primero que tenemos que hacer.
F = 50 N
m = 13,000 gramos
a = ?
Hacemos la conversión de los gramos a kilogramos, ya que son las unidades del sistema internacional.
Despejando la aceleración de la fórmula de la segunda ley de Newton, tenemos:
Que vendría a ser nuestro resultado.
TERCERA LEY DE NEWTON
La tercera ley de Newton o principio de acción y reacción establece que: si dos objetos llamados  y
y  interactúan, la fuerza
interactúan, la fuerza  ejercida por el objeto
ejercida por el objeto  sobre el objeto
sobre el objeto  es igual en magnitud y opuesta en dirección a la fuerza
es igual en magnitud y opuesta en dirección a la fuerza  ejercida por el objeto
ejercida por el objeto  sobre el objeto
sobre el objeto  . Así, se puede expresar:
. Así, se puede expresar:
Tercera Ley de Newton
Siempre que un objeto ejerce una fuerza (acción) sobre otro, el segundo objeto ejerce sobre el primero una fuerza (reacción) de igual magnitud, en la misma dirección, pero de sentido contrario.
Siempre que un objeto ejerce una fuerza (acción) sobre otro, el segundo objeto ejerce sobre el primero una fuerza (reacción) de igual magnitud, en la misma dirección, pero de sentido contrario.
La fuerza que el objeto  aplica sobre el objeto
aplica sobre el objeto  se conoce como acción y la fuerza que el objeto
se conoce como acción y la fuerza que el objeto  aplica sobre e objeto
aplica sobre e objeto  se conoce como reacción. La fuerza de acción tiene la misma magnitud que la fuerza de reacción, pero en dirección opuesta.
se conoce como reacción. La fuerza de acción tiene la misma magnitud que la fuerza de reacción, pero en dirección opuesta.
La tercera ley de Newton expresa que las fuerzas siempre se presentan en pares, es decir, no puede existir una fuerza aislada. Además, estas fuerzas actúan sobre objetos diferentes, por esta razón no se anulan entre sí.

Por ejemplo, la fuerza que la Tierra ejerce sobre la Luna,  , es igual en magnitud y opuesta en dirección a la fuerza que la Luna ejerce sobre la Tierra,
, es igual en magnitud y opuesta en dirección a la fuerza que la Luna ejerce sobre la Tierra,  .
.
Un futbolista patea una pelota
de masa 0,5 Kg con una aceleración de 2 m/s^2 y una dirección al eje X positivo.
Determinar la fuerza de reacción que siente el pie del futbolista.
Se
aplica la ecuación de la fuerza para determinar el módulo de la misma
Fuerza
= masa * aceleración
F = 0,5
* 2 = 1N
El
vector fuerza será:
Vf =
(1,0) N
Por lo
tanto la reacción que es ejercida sobre el pie del futbolista es:
Reacción
del Vf = - Vf = (-1,0) N
SISTEMA DE REFERENCIA INERCIAL
El sistema que define a los sistemas inerciales está de acuerdo con el principio de Albert Einstein que afirma que los sistemas inerciales son propiedad absoluta y comparten los beneficios de las leyes físicas. En los términos más prácticos las propiedades que se aseveran en este artículo no son más que una conceptualización de lo referente a la equivalencia de los sistemas y sus referencias acreditadas. En efecto uno de los grandes dilemas de la humanidad fue siempre determinar cuales eran las fuerzas aplicadas por la inercia y Einstein fue uno de los hombres que pudo esclarecer este trabajo de una forma bastante particular.
En mecánica newtoniana, un sistema de referencia inercial es un sistema de referencia en el que las leyes del movimiento cumplen las leyes de Newton y, por tanto, la variación del momento lineal del sistema es igual a las fuerzas reales sobre el sistema.
LEY DE HOOKE
¿Cómo medir Fuerzas?
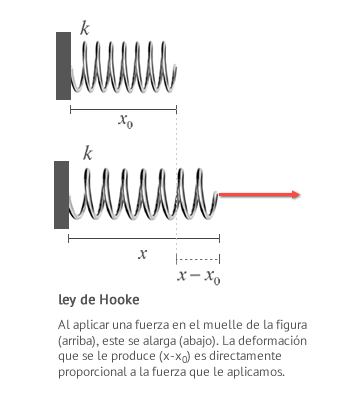
Cuando aplicas una fuerza a un muelle, probablemente este se alargará. Si duplicas la fuerza, el alargamiento también se duplicará. Esto es lo que se conoce como la ley de Hooke.
La ley de Hooke establece que el alargamiento de un muelle es directamente proporcional al módulo de la fuerza que se le aplique, siempre y cuando no se deforme permanentemente dicho muelle.
donde:
- F es el módulo de la fuerza que se aplica sobre el muelle.
- k es la constante elástica del muelle, que relaciona fuerza y alargamiento. Cuanto mayor es su valor más trabajo costará estirar el muelle. Depende del muelle, de tal forma que cada uno tendrá la suya propia.
- x0 es la longitud del muelle sin aplicar la fuerza.
- x es la longitud del muelle con la fuerza aplicada.
Si al aplicar la fuerza, deformamos permanentemente el muelle decimos que hemos superado su límite de elasticidad.
PLANO INCLINADO
El plano inclinado es una máquina simple que permite subir objetos realizando menos fuerza. Para calcular la tensión de la cuerda que equilibra el plano, descomponemos las fuerzas y hacemos la sumatoria sobre cada eje. Es recomendable girar el sistema de ejes de tal forma que uno de ellos quede paralelo al plano. Con esto se simplifican las cuentas ya que la sumatoria de fuerzas en X tiene el mismo ángulo que la tensión que lo equilibra.

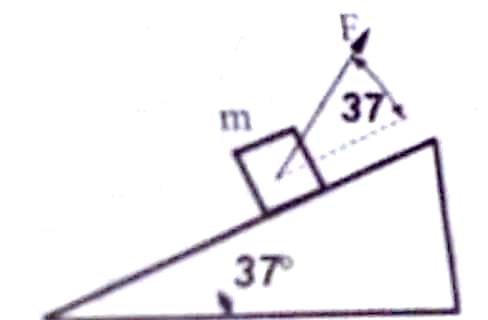
EJERCICIO 1
Un cuerpo de masa m = 60 kg, está apoyado sobre un plano inclinado de 37° tal y como muestra la figura. El módulo de la fuerza F es de 500 N. calcule la aceleración del bloque. El sistema está libre de rozamiento.
Comenzamos con la fórmula vista en la teoría:
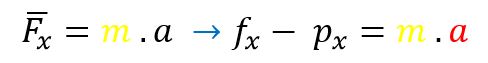
Ahora, reemplazamos con los datos que nos brinda el enunciado:
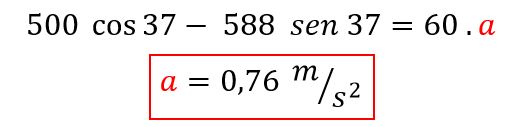
La aceleración del bloque será de 0,76 m/s2
EJERCICIO 2
Calcule la aceleración de cada bloque y el esfuerzo que hace la cuerda que conecta ambos bloques.
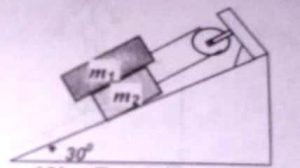
Los datos son los siguientes:
m1 = 20 kg; m2 = 10 kg; Todas las superficies carecen de fricción.
Primero, comenzaremos calculando m1
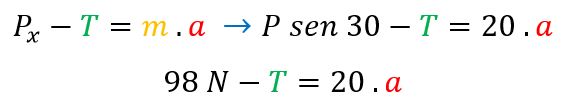
Ahora, continuamos con m2
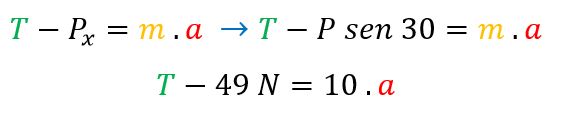
Una vez que obtenemos las dos ecuaciones de m1 y m2, podemos sumar los resultados:
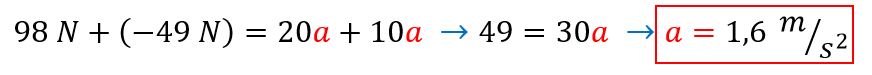
Ahora que conocemos a podremos calcular el esfuerzo que se realiza:
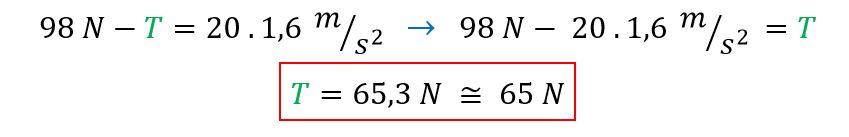
Entonces, la aceleración de cada bloque es de 1,6 m/s2 y el esfuerzo que hace con la cuerda es de aproximadamente 65 N




Comentarios
Publicar un comentario